Introduction à l'analyse mathématique - Théorie des ensembles

📘 Analyse mathématique : notions fondamentales sur les ensembles

Ce document complet propose une exploration détaillée des notions fondamentales sur les ensembles, indispensable pour toute personne qui débute ou souhaite consolider ses bases en analyse mathématique. Les ensembles constituent le langage universel des mathématiques modernes : ils permettent de formaliser des concepts variés, de la simple manipulation de données à l’élaboration de structures abstraites.

Dans ce fichier, nous abordons en profondeur les principales opérations et relations qui régissent les ensembles, avec des explications claires, des illustrations schématiques et de nombreux exemples concrets. Chaque notion est accompagnée d’exercices corrigés, permettant non seulement de comprendre la théorie, mais aussi de savoir l’appliquer efficacement dans différents contextes académiques et pratiques.

📌 Contenu détaillé :

• 🔹 Inclusion et égalité : comprendre comment comparer deux ensembles, déterminer si l’un est inclus dans l’autre, et maîtriser les conditions d’égalité entre ensembles.
• 🔹 Réunion et intersection : savoir combiner les éléments de plusieurs ensembles, identifier leurs points communs et leurs différences.
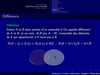
• 🔹 Complémentaire et différence : manipuler ce qui se trouve “à l’extérieur” d’un ensemble et soustraire les éléments d’un autre.
• 🔹 Différence symétrique : analyser les éléments qui appartiennent à l’un ou à l’autre, mais pas aux deux à la fois.
• 🔹 Produit cartésien : introduire la notion de paires ordonnées et comprendre son rôle dans la construction de relations et fonctions.

🎯 Objectif : Acquérir une vision globale et précise de la théorie des ensembles, base incontournable pour la logique mathématique, l’algèbre, l’analyse et même l’informatique.