𝙼𝚊𝚋𝚕𝚎
𝙼𝚊𝚋𝚕𝚎
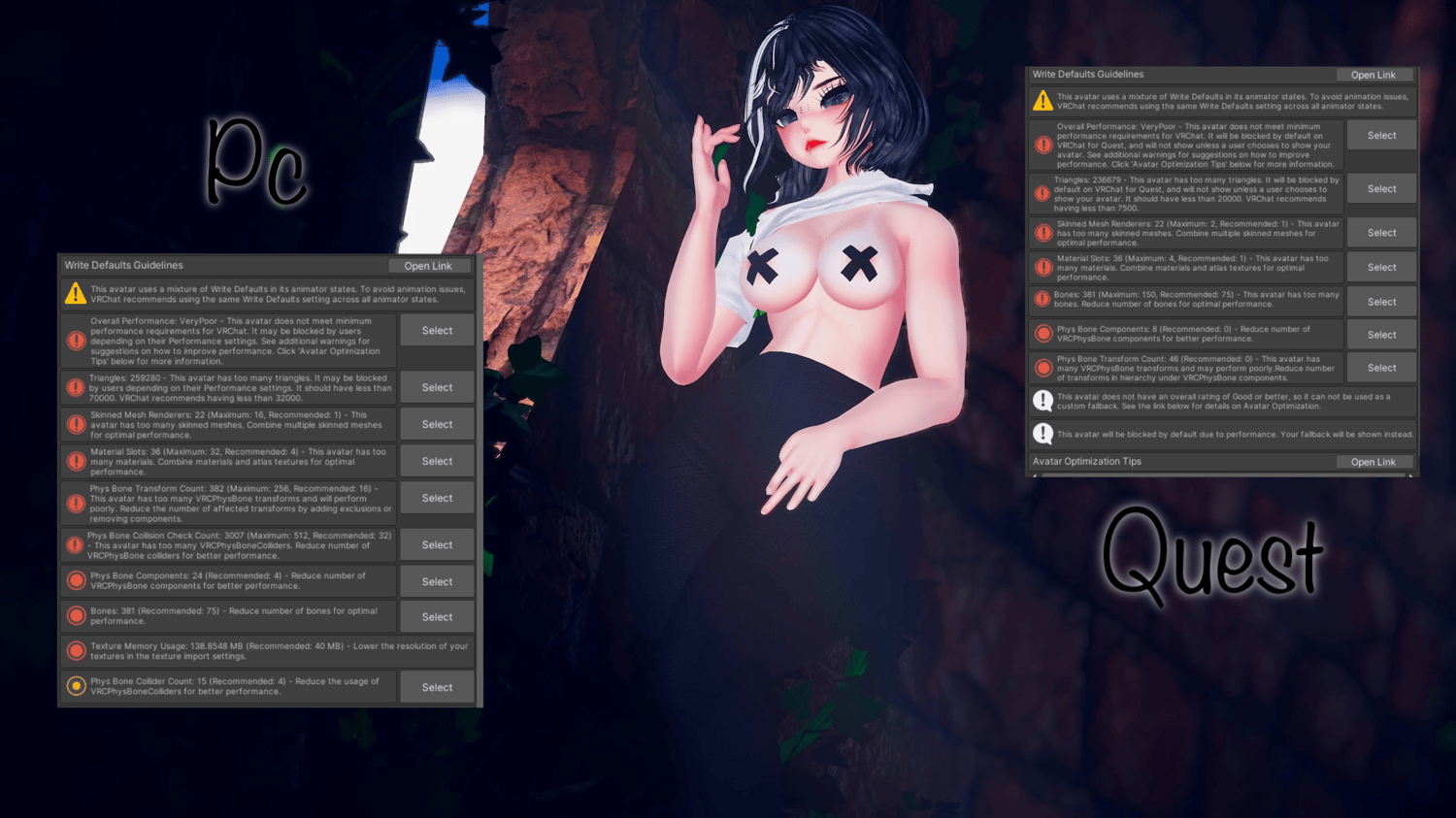
𝚂𝚏𝚠 𝙿𝚌+𝚀𝚞𝚎𝚜𝚝
𝚃𝚑𝚒𝚜 𝚊𝚟𝚊𝚝𝚊𝚛 𝚒𝚜 𝚊 𝚗𝚒𝚝𝚛𝚘 𝚏𝚛𝚎𝚎𝚋𝚒𝚎! 𝙱𝚘𝚘𝚜𝚝 𝚖𝚢 𝚍𝚒𝚜𝚌𝚘𝚛𝚍 𝚝𝚘 𝚐𝚎𝚝 𝚑𝚎𝚛 𝚏𝚛𝚎𝚎!
𝙳𝚒𝚜𝚌𝚘𝚛𝚍: 𝚑𝚝𝚝𝚙𝚜://𝚍𝚒𝚜𝚌𝚘𝚛𝚍.𝚐𝚐/𝚜𝚝𝚊𝚢𝚕𝚘𝚠𝚔𝚎𝚢
𝚄𝚙𝚕𝚘𝚊𝚍 𝙸𝚗𝚜𝚝𝚛𝚞𝚌𝚝𝚒𝚘𝚗𝚜 𝙿𝚌: (𝚄𝚗𝚒𝚝𝚢 𝟸0𝟸𝟸 𝚆𝚘𝚛𝚔𝚜)
𝟷:𝙸𝚗𝚜𝚝𝚎𝚛𝚝 𝙿𝚘𝚒 𝚅𝚎𝚛 𝟽.𝟹.𝟻0 𝚝𝚘 𝙻𝚊𝚝𝚎𝚜𝚝
𝟸:𝙰𝚟𝚊𝚝𝚊𝚛 𝙿𝚊𝚌𝚔𝚊𝚐𝚎
𝟹:𝚁𝚎𝚖𝚘𝚟𝚎 𝙱𝚕𝚞𝚎𝚙𝚛𝚒𝚗𝚝 𝙸𝚍
𝟺:𝙷𝚒𝚝 𝙱𝚞𝚒𝚕𝚍 𝚊𝚗𝚍 𝙿𝚞𝚋𝚕𝚒𝚜𝚑 𝙵𝚘𝚛 𝚆𝚒𝚗𝚍𝚘𝚠𝚜
𝟻:𝙸𝚏 𝚢𝚘𝚞 𝚠𝚊𝚗𝚝 𝚊 𝚌𝚞𝚜𝚝𝚘𝚖 𝚙𝚑𝚘𝚝𝚘 𝚊𝚍𝚍 𝚝𝚑𝚎 𝚙𝚑𝚘𝚝𝚘 𝚊𝚍𝚍𝚎𝚍 𝚒𝚗 𝚝𝚑𝚎 𝚍𝚘𝚠𝚗𝚕𝚘𝚊𝚍 𝚊𝚛𝚎𝚊 <𝟹
𝟼:𝚂𝚎𝚝 𝚝𝚘 𝙿𝚁𝙸𝚅𝙰𝚃𝙴 𝚊𝚗𝚍 𝚄𝚙𝚕𝚘𝚊𝚍!
𝚄𝚙𝚕𝚘𝚊𝚍 𝙸𝚗𝚜𝚝𝚛𝚞𝚌𝚝𝚒𝚘𝚗𝚜 𝚀𝚞𝚎𝚜𝚝: (𝚄𝚗𝚒𝚝𝚢 𝟸0𝟸𝟸 𝚆𝚘𝚛𝚔𝚜)
(𝙼𝚄𝚂𝚃 𝙱𝙴 𝙽𝙴𝚆 𝙿𝚁𝙾𝙹𝙴𝙲𝚃)
𝟷:𝙲𝚑𝚊𝚗𝚐𝚎 𝙱𝚞𝚒𝚕𝚍 𝚃𝚊𝚛𝚐𝚎𝚝 𝚃𝚘 𝙰𝚗𝚍𝚛𝚘𝚒𝚍
𝟸:𝙰𝚟𝚊𝚝𝚊𝚛 𝚙𝚊𝚌𝚔𝚊𝚐𝚎
𝟹:𝙰𝚍𝚍 𝙱𝚕𝚞𝚎𝚙𝚛𝚒𝚗𝚝 𝙸𝚍 𝚘𝚏 𝙿𝚌 𝚅𝚎𝚛𝚜𝚒𝚘𝚗
𝟺:𝙷𝚒𝚝 𝙱𝚞𝚒𝚕𝚍 𝚊𝚗𝚍 𝙿𝚞𝚋𝚕𝚒𝚜𝚑 𝙵𝚘𝚛 𝙰𝚗𝚍𝚛𝚘𝚒𝚍
𝙽𝚘𝚝 𝚊𝚟𝚊𝚒𝚕𝚊𝚋𝚕𝚎 𝚘𝚗 𝚚𝚞𝚎𝚜𝚝:
𝙸𝚏 𝚢𝚘𝚞 𝚠𝚘𝚞𝚕𝚍 𝚕𝚒𝚔𝚎 𝚝𝚘 𝚞𝚜𝚎 𝚝𝚑𝚎𝚜𝚎 𝚊𝚜𝚜𝚎𝚝𝚜 𝙿𝚕𝚎𝚊𝚜𝚎 𝚐𝚘 𝚝𝚘 𝚝𝚑𝚎𝚒𝚛 𝚙𝚊𝚐𝚎
𝙸𝚏 𝚢𝚘𝚞 𝚗𝚎𝚎𝚍 𝚑𝚎𝚕𝚙 𝚛𝚎𝚊𝚌𝚑 𝚖𝚎 𝚊𝚋𝚘𝚞𝚝 𝚊𝚗𝚢 𝚒𝚜𝚜𝚞𝚎𝚜 𝚢𝚘𝚞𝚛 𝚑𝚊𝚟𝚒𝚗𝚐. 𝚃𝚒𝚌𝚔𝚎𝚝 𝚘𝚛 𝙳𝚖𝚜, 𝙱𝚘𝚝𝚑 𝚠𝚘𝚛𝚔.
𝚃𝚘𝚜: 𝙳𝙾 𝙽𝙾𝚃 𝚄𝚜𝚎 𝚝𝚑𝚎 𝚊𝚜𝚜𝚎𝚝𝚜 𝚏𝚛𝚘𝚖 𝚖𝚢 𝚊𝚟𝚊𝚝𝚊𝚛 𝚠𝚒𝚝𝚑𝚘𝚞𝚝 𝚐𝚎𝚝𝚝𝚒𝚗𝚐 𝚝𝚑𝚎𝚖 𝚏𝚛𝚘𝚖 𝚝𝚑𝚎 𝚘𝚠𝚗𝚎𝚛𝚜. 𝙵𝚘𝚛 𝚊𝚗𝚢 𝚛𝚎𝚊𝚜𝚘𝚗!
𝙳𝙾 𝙽𝙾𝚃 𝙴𝚍𝚒𝚝 𝚝𝚑𝚒𝚜 𝚊𝚟𝚊𝚝𝚊𝚛 𝚊𝚗𝚍 𝚜𝚎𝚕𝚕 𝚒𝚝 𝚊𝚜 𝚢𝚘𝚞𝚛 𝚘𝚠𝚗 (𝚏𝚛𝚎𝚎 𝚘𝚛 𝚙𝚊𝚒𝚍 𝚍𝚘𝚎𝚜𝚗'𝚝 𝚖𝚊𝚝𝚝𝚎𝚛)
𝙳𝙾 𝙽𝙾𝚃 𝚂𝚎𝚝 𝚝𝚑𝚒𝚜 𝚊𝚜 𝙿𝚞𝚋𝚕𝚒𝚌
𝙳𝙾 𝙽𝙾𝚃 𝚄𝚙𝚕𝚘𝚊𝚍 𝚝𝚘 𝚜𝚘𝚖𝚎𝚘𝚗𝚎'𝚜 𝚊𝚌𝚌𝚘𝚞𝚗𝚝 𝚠𝚒𝚝𝚑𝚘𝚞𝚝 𝚝𝚑𝚎𝚖 𝚋𝚞𝚢𝚒𝚗𝚐 𝚒𝚝 𝚏𝚛𝚘𝚖 𝚖𝚎 𝚏𝚒𝚛𝚜𝚝.
𝙷𝚢𝚙𝚎𝚛𝙻𝚒𝚗𝚔𝚜 𝚟𝚟𝚟
𝙲𝚕𝚘𝚝𝚑𝚒𝚗𝚐 𝚊𝚗𝚍 𝙰𝚗𝚍 𝙰𝚌𝚌𝚎𝚜𝚜𝚘𝚛𝚢 𝙲𝚛𝚎𝚍𝚒𝚝𝚜
𝙱𝚘𝚘𝚝 𝚂𝚎𝚝 (𝙽𝚒𝚝𝚛𝚘, 𝙽𝚘𝚝 𝙰𝚟𝚊𝚒𝚕𝚊𝚋𝚕𝚎 𝙰𝚗𝚢𝚖𝚘𝚛𝚎)
𝙿𝚊𝚜𝚝𝚒𝚎𝚜 𝚋𝚢 𝚖𝚎 (𝙽𝚘𝚝 𝚊𝚟𝚊𝚒𝚕𝚊𝚋𝚕𝚎)
𝙱𝚊𝚜𝚎 𝙲𝚛𝚎𝚍𝚒𝚝𝚜
𝚄𝚗𝚒𝚝𝚢 𝙲𝚛𝚎𝚍𝚒𝚝𝚜
𝙸𝚏 𝚢𝚘𝚞 𝚊𝚛𝚎 𝚝𝚑𝚎 𝚌𝚛𝚎𝚊𝚝𝚘𝚛 𝚘𝚏 𝚘𝚗𝚎 𝚘𝚏 𝚝𝚑𝚎𝚜𝚎 𝚊𝚗𝚍 𝙸 𝚗𝚎𝚎𝚍 𝚝𝚘 𝚌𝚑𝚊𝚗𝚐𝚎 𝚝𝚑𝚎 𝚜𝚑𝚘𝚙 𝚗𝚊𝚖𝚎 𝚘𝚛 𝚒𝚏 𝚒𝚝𝚜 𝚠𝚛𝚘𝚗𝚐𝚕𝚢 𝚗𝚊𝚖𝚎𝚍 𝚊𝚗𝚍 𝚕𝚒𝚗𝚔𝚎𝚍 𝚙𝚕𝚎𝚊𝚜𝚎 𝚖𝚊𝚔𝚎 𝚊 𝚝𝚒𝚌𝚔𝚎𝚝 𝚒𝚗 𝚖𝚢 𝚍𝚒𝚜𝚌𝚘𝚛𝚍 𝚠𝚒𝚝𝚑 𝚙𝚛𝚘𝚘𝚏 <𝟹