Video Training, Excel Workbook & Guide

Plus C++ & Python Sourcecode

Contents

MonteCarlo.xlsm - Excel Workbook

MonteCarlo.pdf - PowerPoint PDF Guide

MonteCarlo.cpp - C++ Sourcecode

MonteCarlo.ipynb - Python Jupyter Notebook

Master Monte Carlo Simulation for Option Pricing

— From Theory to Code

This complete training pack takes you step‑by‑step through stochastic calculus, risk‑neutral pricing, and martingales, while giving you hands‑on tools to simulate and price options. With PowerPoint slides, an interactive Excel workbook, and fully functional C++ and Python source code, you’ll learn not only the math behind Monte Carlo but also how to implement it, test convergence, and tackle exotic barrier options with confidence.

Video Training

The video training covers the theory behind monte carlo simulation with practical examples on how to price vanilla and exotic options. Suitable for trading, sales, structurers, quants and finance professionals as well as students.

Video Link (33 mins)

https://www.youtube.com/watch?v=xdBHMLZa2rw

PowerPoint Training Slides & Excel Workbook

This pack includes a structured training guide in PowerPoint format that introduces the mathematical foundations and stochastic calculus techniques used in quantitative finance. We cover key concepts such as Geometric Brownian Motion (GBM), stochastic differential equations, martingales, the Girsanov Theorem, and risk-neutral pricing. Each concept is illustrated with intuitive examples and practical applications in option pricing.

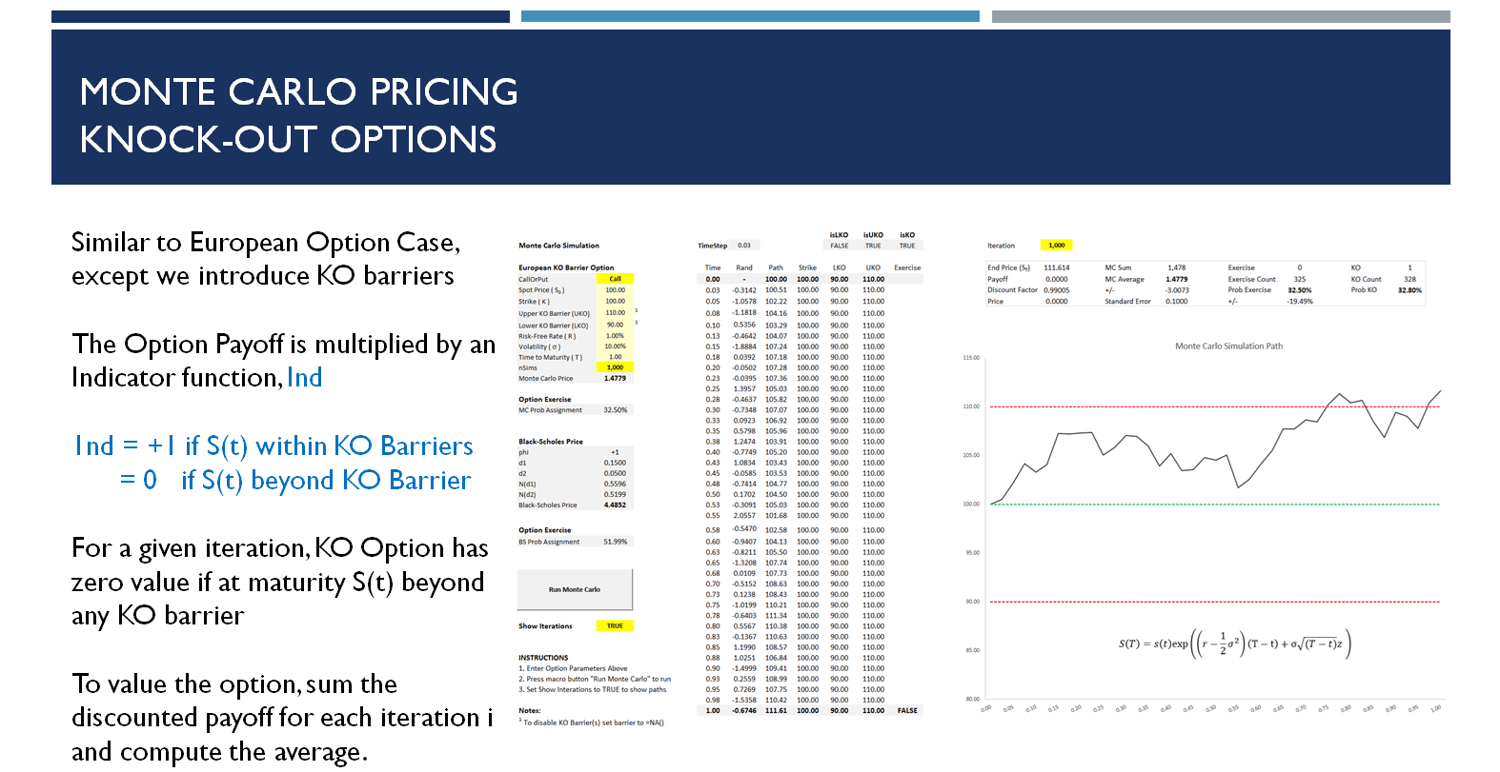
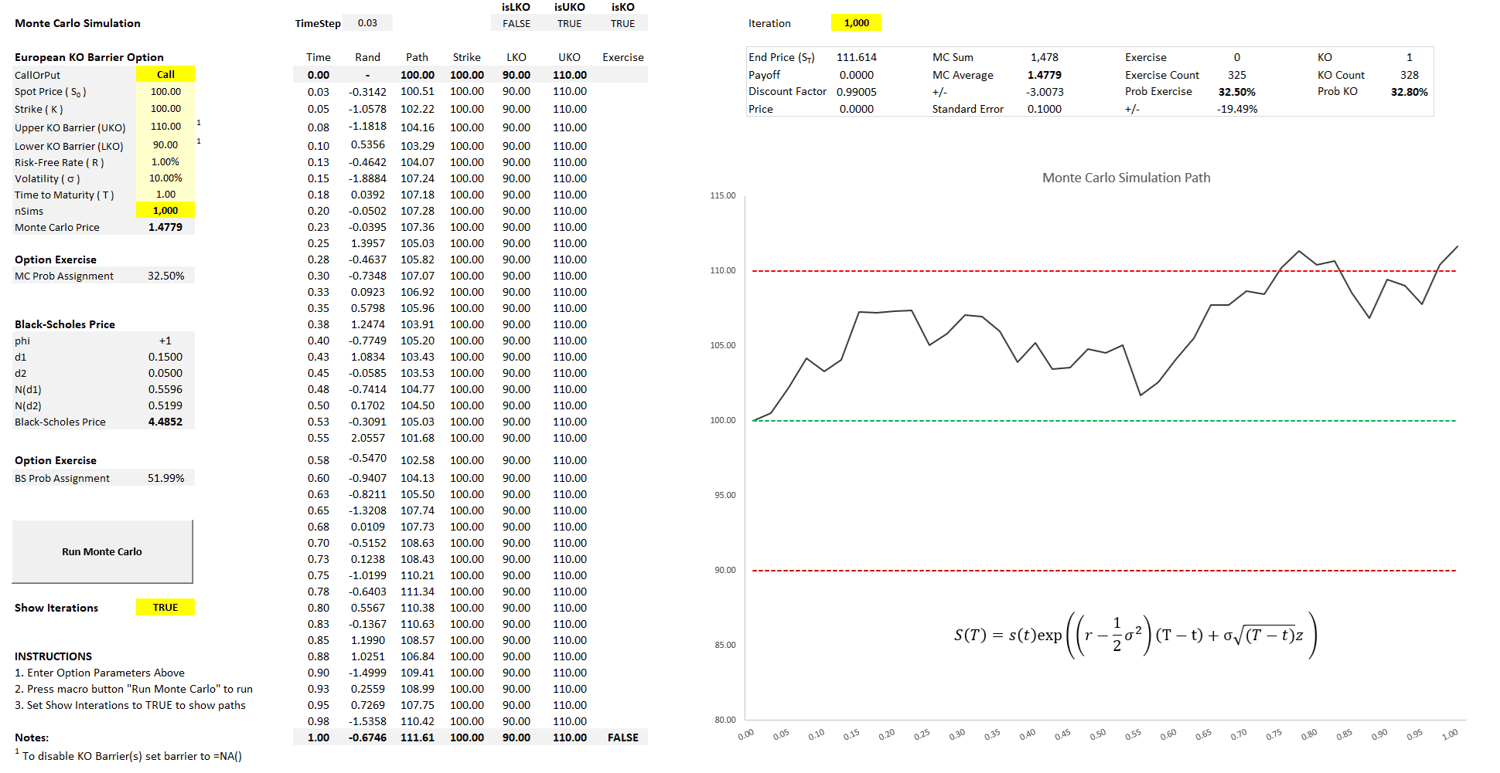
To complement the theory, the Excel workbook provides a fully functional Monte Carlo pricer with step‑by‑step instructions and clean visuals. You will simulate European call options, verify results against the closed‑form Black–Scholes formula, and even calculate the probability of exercise through Monte Carlo – comparing this directly to the classical N(d2). Going beyond vanilla options, the Excel demo also extends to more advanced products such as Double Knock‑Out (barrier) options, showing how Monte Carlo methods can handle exotic payoffs in a clear, visual, and hands‑on way.

C++ and Python Sourcecode

For those who prefer coding over spreadsheets, the included C++ and Python implementations bring the Monte Carlo simulations to life in a programming environment. The C++ source code demonstrates how to implement Black–Scholes option pricing, build a robust Normal CDF using the error function (erf) approach, and generate high‑quality random numbers using the Mersenne Twister. We emphasize convergence testing so you can see in practice how accuracy improves with more simulations.

The Python Jupyter Notebook offers an equally powerful and accessible environment, ideal for quick experimentation and plotting. You will reproduce the European option pricing simulations, generate detailed payoff distributions, and visualize convergence using increasing numbers of simulations. Confidence intervals and error bounds are introduced to highlight statistical precision, and plots make interpretation clear and insightful.

Both the C++ and Python code provide reusable templates you can adapt for more complex pricing or trading strategies.

Keywords: Monte Carlo, Simulation, Training Guide, Geometric Brownian Motion, GBM, Stochastic Differential Equations, Change of Measure, Girsanov Theorem, Risk-Neutral Pricing, Martingales, Arbitrage Free, Martingale Representation Theorem, Practical Examples, Excel, C+, Python, Option Pricing, European Option, Barrier Options, Knock-Out Options, KO