Golden Ratio Wrap Knitting Pattern
On Sale
$5.95
$5.95
The Golden Ratio is a place where art meets math.
Did You Know?
We find the golden ratio when we divide a line into two parts so that the whole length divided by the long part is also equal to the long part divided by the short part. This ratio is usually rounded to 1:1.618.
How Does it Work?
Shapes and designs created using this ratio are famously aesthetically appealing, so what better place to start for a beautiful wrap or lap blanket than a so-called golden rectangle where the long edge is (as close as we can get in knitting to) 1.618 x the short side? And to demonstrate some of the other fascinating properties of this ratio, how about we construct this by adding together squares?
A golden rectangle with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a.
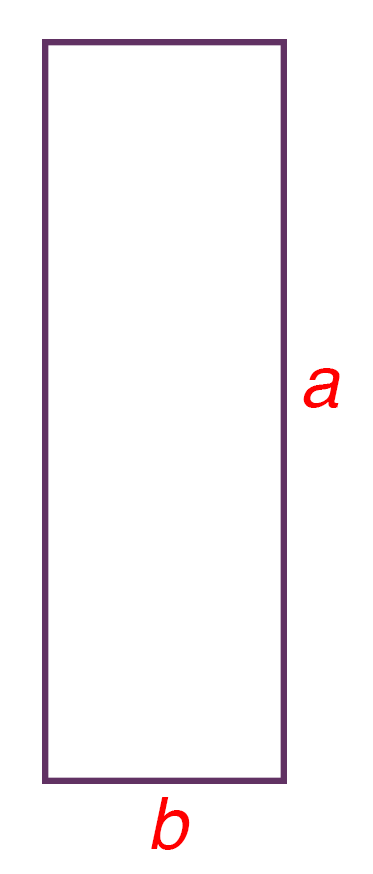

And to make things even more interesting, the decrease lines at the center of the mitered squares are used to approximate the line of a golden spiral (sorry folks, I couldn’t think of a way to make curved line!).
For a final layer of mathematical deliciousness, color changes are used within each square to mark the division of the line of the edge with the golden ratio (as accurately as one can in knitting)!
Options are provided for 2 sizes and three gauges: the smaller (S) wrap/baby blanket is worked in fingering and the large wrap/lap blanket is worked in either DK (M) or worsted (L).
Did You Know?
We find the golden ratio when we divide a line into two parts so that the whole length divided by the long part is also equal to the long part divided by the short part. This ratio is usually rounded to 1:1.618.
How Does it Work?
Shapes and designs created using this ratio are famously aesthetically appealing, so what better place to start for a beautiful wrap or lap blanket than a so-called golden rectangle where the long edge is (as close as we can get in knitting to) 1.618 x the short side? And to demonstrate some of the other fascinating properties of this ratio, how about we construct this by adding together squares?
A golden rectangle with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a.


And to make things even more interesting, the decrease lines at the center of the mitered squares are used to approximate the line of a golden spiral (sorry folks, I couldn’t think of a way to make curved line!).
For a final layer of mathematical deliciousness, color changes are used within each square to mark the division of the line of the edge with the golden ratio (as accurately as one can in knitting)!
Options are provided for 2 sizes and three gauges: the smaller (S) wrap/baby blanket is worked in fingering and the large wrap/lap blanket is worked in either DK (M) or worsted (L).






















