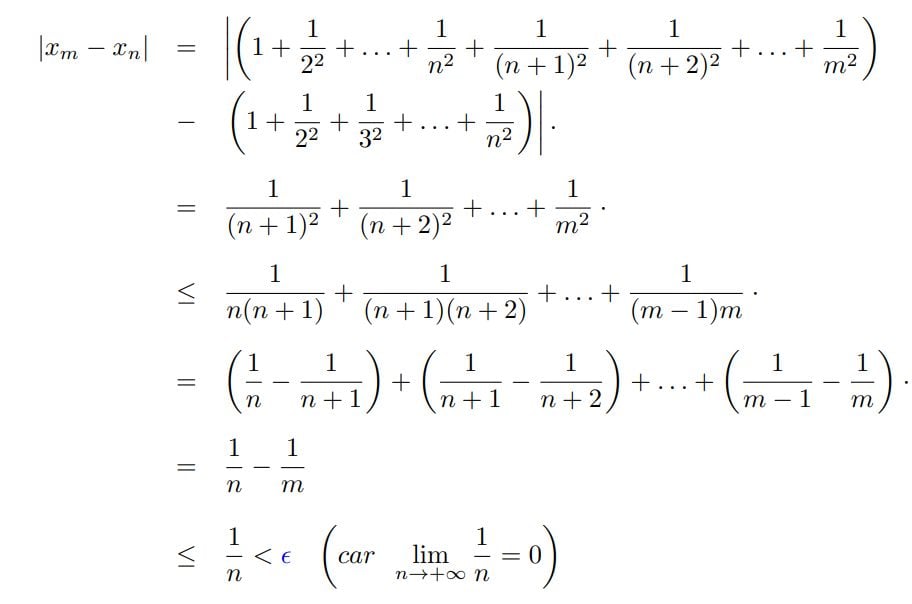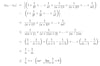Dans ce fichier, je t’explique le critère de Cauchy pour les suites numériques.

🔍 **Contenu du fichier** :  

- Définition rigoureuse du critère  

- Proposition avec démonstration  

- Plusieurs exercices corrigés pas à pas 

🎓 Objectif : T’aider à prouver et utiliser ce critère sans stress, que ce soit en L1 math, ou préparation aux examens.

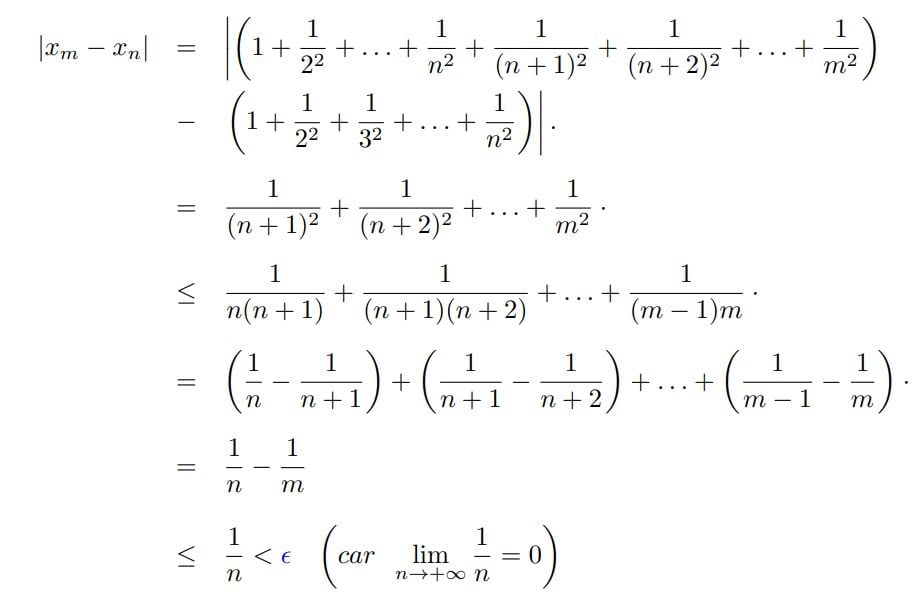
Ce fichier PDF constitue une ressource essentielle pour tout·e étudiant·e souhaitant réviser de manière efficace la théorie des semi-groupes d’opérateurs. Ce chapitre clé de l’analyse fonctionnelle est fondamental pour comprendre et analyser l’évolution de systèmes complexes à travers les équations différentielles et les systèmes dynamiques.

Le document présente un examen final complet avec ses corrections détaillées. L’objectif est double : te permettre de maîtriser les méthodes de résolution et te montrer comment structurer des réponses claires et rigoureuses dans un cadre académique. Chaque solution est expliquée pas à pas, avec des rappels théoriques lorsque nécessaire, pour renforcer tes connaissances et éviter les erreurs fréquentes.

📌 Ce que tu trouveras dans ce fichier :

• Résolution méthodique de chaque exercice.
• Explications commentées illustrant le raisonnement logique derrière chaque démarche.

Ce format écrit est idéal si tu préfères étudier à ton rythme, annoter, surligner ou revenir sur des points précis selon tes besoins. En travaillant avec ce fichier, tu consolideras tes bases, amélioreras ta compréhension et développeras ta capacité à restituer tes connaissances de manière structurée et convaincante le jour de l’examen.

Cette fiche propose une série complète d’exercices corrigés sur la théorie des ensembles, pensée pour une révision rapide mais profonde. L’approche combine rigueur et pédagogie : chaque exercice est suivi d’une correction détaillée qui explique non seulement le “quoi”, mais surtout le “pourquoi” et le “comment”.

🔎 Au programme

• Notations et opérations de base : union, intersection, différence, complémentaire
• Relations d’appartenance et inclusion, sous-ensembles et familles d’ensembles
• Opérations sur les ensembles finis et infinis, principe d’induction simple
• Partitions, produit cartésien et applications entre ensembles
• Exercices sur les ensembles de nombres (ℕ, ℤ, ℚ, ℝ) et manipulations fréquentes
• Problèmes types d’examen avec stratégies de résolution

🎯 Ce que tu gagnes

En travaillant cette fiche tu vas :

• Renforcer ta maîtrise des notations et de la logique des ensembles
• Apprendre à structurer une démonstration claire et concise
• Reconnaître les pièges classiques et savoir les éviter
• Gagner en rapidité pour les contrôles grâce à des méthodes réutilisables

👥 Public visé

Étudiants en licence (SM, MI, ST), classes préparatoires, ou toute personne souhaitant consolider ses bases en mathématiques discrètes et analyse élémentaire.